[最新] (a+b+c)^3 expansion formula 268121-(a+b)^3 expansion formula
(a b) 1 = a b (a b) 2 = (a b) * (a b) = a 2 2ab b 2;Explanation Binomial formula for (a b)3 ⇒3 C0a3b0 3 C1a2b1 3 C2a1b2 3 C3a0b3 Here, a = x and b = 1 ⇒3 C0x3 3 C1x2 × 11 3 C2x1 ×12 3 C3 × 13 As →3 C0 =3 C3 = 1 and →3 C1 =3 C2 = 3 ⇒ x3 3x2 3x 1In mathematics, a trinomial expansion is the expansion of a power of a sum of three terms into monomials The expansion is given by The expansion is given by ( a b c ) n = ∑ i j k = n i , j , k ( n i , j , k ) a i b j c k , {\displaystyle (abc)^{n}=\sum _{\stackrel {i,j,k}{ijk=n}}{n \choose i,j,k}\,a^{i}\,b^{\;\!j}\;\!c^{k},}

Graph Graph Equations And Equation Systems With Step By Step Math Problem Solver
(a+b)^3 expansion formula
(a+b)^3 expansion formula-= a4 4a3x6a2x2 4ax3 x4 In general we see that the coe cients of (a x) n come from the nth row of Pascal's riangleT , in which each term is the sum of the two terms just above itWhat I want to do with this video is cover something called the triple product expansion or Lagrange's formula, sometimes And it's really just a simplification of the cross product of three vectors, so if I take the cross product of a, and then b cross c


The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets
A 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) If (a b c) = 0, a 3 b 3 c 3 = 3abcThe Formula is given below (a b c)³ = a³ b³ c³ 3 (a b) (b c) (a c)= (a b)(a b)(a b) = (a b)(a² ab ab b²) = (a b)(a² 2ab b²) = a³ 2a²b ab² a²b 2ab² b³ = a³ 3a²b 3ab² b³ Answer a³ 3a²b 3ab² b³= (a b)(a b)(a b) = (a b)(a² ab ab b²) = (a b)(a² 2ab b²) = a³ 2a²b ab² a²b 2ab² b³ = a³ 3a²b 3ab² b³
$$(a b c)^3 = (a^3 b^3 c^3) (3a^2b 3a^2c 3abc) (3ab^2 3b^2c 3abc) (3ac^2 3bc^2 3abc) 3abc$$ $$(a b c)^3 = (a^3 b^3 c^3) 3a(ab ac bc) 3b(ab bc ac) 3c(ac bc ab) 3abc$$3 (abc)2=a2b2c22(abbcca) 4 (ab)3=a3b33ab(ab);a3b3=(ab)−3ab(ab) 5 (a−b)3=a3−b3−3ab(a−b);a3−b3=(a−b)33ab(a−b) 6a2−b2=(ab)(a−b) 7a3−b3=(a−b)(a2abb2) 8a3b3=(ab)(a2−abb2) 9an−bn=(a−b)(an−1a−2ban−3b2 bn−1) 10an=aaantimes 11aman=am 12A^3 b^3 c^3 3abc = (a b c) (a^2 b^2 c^2 ab ac bc) By assumption a^3b^3c^3=3abc so the left hand side is 0 Therefore (abc) (a^2b^2c^2abacbc) = 0 So either abc=0 or
(say, a;b) to functions in the new variable z, whose domain is an interval of 2ˇlength This is because x= a)z= ˇ l aand x= b)z= ˇ l b= 2 b a (b a a) = 2ˇ ˇ l a Thus when the variable xin f(x) moves from ato b, the new variable zin the new function F(z) (which is the same function fin the new variable) moves from cto c2ˇ, where c= ˇ l a\(=> (abc)^3 = (a^3ab^2ac^2 2a^2b 2abc 2ca^2)\\ (a^2bb^3bc^2 2ab^2 2b^2c 2abc)\\ c \times (a^2b^2c^2 2ab 2bc 2ca) \) \(=> (abc)^3 = (a^3ab^2ac^2 2a^2b 2abc 2ca^2)\\ (a^2bb^3bc^2 2ab^2 2b^2c 2abc)\\ (ca^2 cb^2 c^3 2abc 2bc^2 2c^2a) \)The cube of sum of the terms a and b or a binomial is written in the following mathematical form in mathematics ( a b) 3 The a plus b whole cube is equal to the a cubed plus b cubed plus three times the product of a, b and sum of a plus b ( a b) 3 = a 3 b 3 3 a b ( a b)


What Is The Formula For Math A B C 3 Math Quora



What Are Various Forms To Write A B C A Whole Cube Quora
(a b) 3 = a 3 b 3 3ab(a b) (a – b) 3 = a 3 – 3a 2 b 3ab 2 – b 3 = a 3 – b 3 – 3ab(a – b) a 3 – b 3 = (a – b)(a 2 ab b 2) a 3 b 3 = (a b)(a 2 – ab b 2) (a b) 4 = a 4 4a 3 b 6a 2 b 2 4ab 3 b 4 (a – b) 4 = a 4 – 4a 3 b 6a 2 b 2 – 4ab 3 b 4;So the answer is 3 3 3 × (3 2 × x) 3 × (x 2 × 3) x 3 (we are replacing a by 3 and b by x in the expansion of (a b) 3 above)B) (a − b) 3 = a 3 − 3a 2 b 3ab 2 − b 3 c) ( x y ) 4 = x 4 4 x 3 y 6 x 2 y 2 4 xy 3 y 4 d) ( x − y ) 4 = x 4 − 4 x 3 y 6 x 2 y 2 − 4 xy 3 y 4



I Am Taking A Taylor Series Expansion Of A Function F X I Wish To Expand The Function Around The Value G X Is This Allowable



How To Develop A Numerical Differentiation Formula Using Taylor Expansion Series Mathematics Stack Exchange
According to this theorem, it is possible to expand the polynomial \((x y)^n\) into a series of the sum involving terms of the form a \(x^b y^c\) Here the exponents b and c are nonnegative integers with condition that b c = n Also, the coefficient of each term is a specific positive integer depending on n and b For example (for n = 4), we have \((xy)^4=x^44x^3y6x^2y^24xy^3y^4\) It is obvious that such expressions and their expansions would be very painful to multiply out by handThe square of the sum of three or more terms can be determined by the formula of the determination of the square of sum of two terms Now we will learn to expand the square of a trinomial (a b c) Let (b c) = x Then (a b c) 2 = (a x) 2 = a 2 2ax x 2Start with a2 b2 = c2 Put in what we know 12 12 = c2 Calculate squares 1 1 = c2 11=2 2 = c2 Swap sides c2 = 2 Square root of both sides c = √2 Which is about c = It works the other way around, too when the three sides of a triangle make a2 b2 = c2, then the triangle is right angled



Expanding Algebraic Expressions Using Identities Worksheets


Boolean Expressions 1 Physical Design Sta Synthesis Dft Automation Flow Dev Verification Services Turnkey Projects
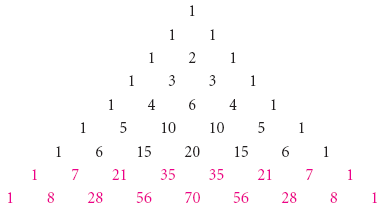
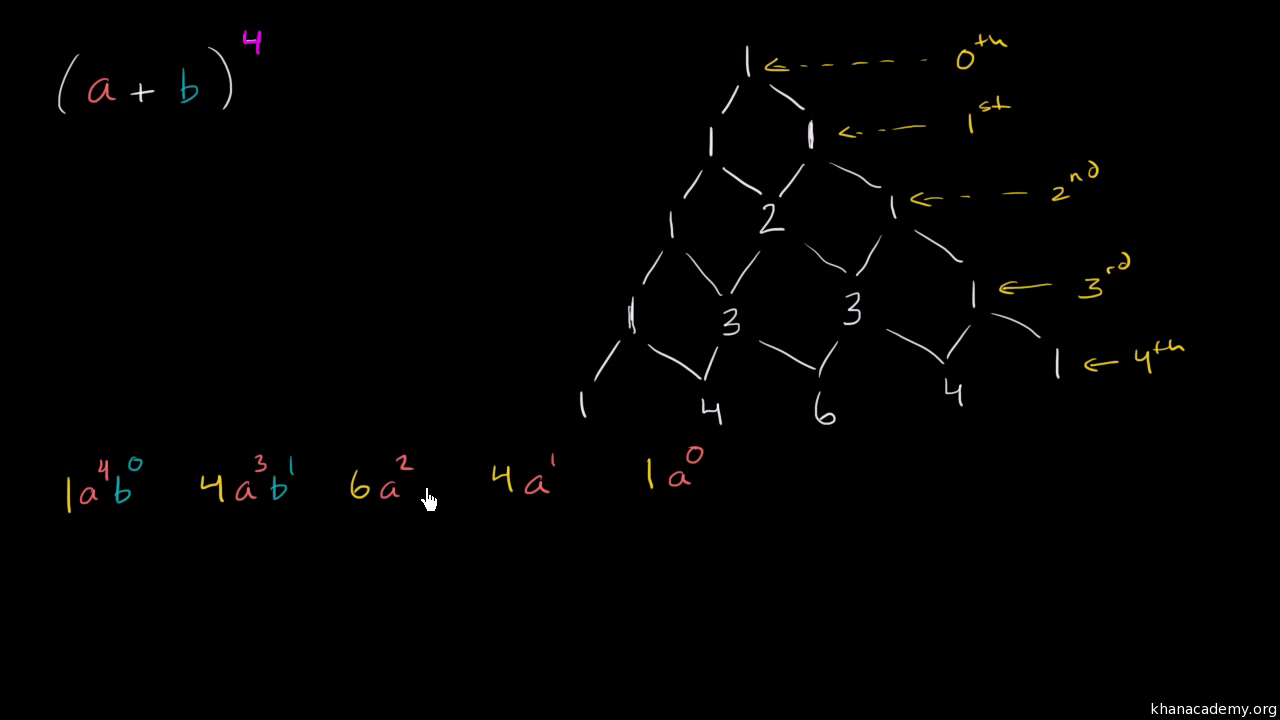
A3 3a2b 3ab2 b3 Now, notice the exponents of a They start at 3 and go down 3, 2, 1, 0 Likewise the exponents of b go upwards 0, 1, 2, 3 If we number the terms 0 to n, we get this k=0 k=1 k=2 k=3Ex a b, a 3 b 3, etc Binomial Theorem Let n ∈ N,x,y,∈ R then n Σ r=0 nC r x n – r · y r nC r x n – r · y r nC n1 x · y n – 1 nC n · y n ie(x y) n = n Σ r=0 nC r x n – r · y r where, Illustration 1 Expand (x/3 2/y) 4 Sol Illustration 2 (√2 1) 5 (√2 − 1) 5 Sol We have5(a b c)2 = a2 b2 c2 2ab2bc 2ca 6(a b c)3 = a3 b3 c33a2b3a2c 3b2c 3b2a 3c2a 3c2a6abc 7a2 b2 = (a b)(a – b ) 8a3 – b3 = (a – b) (a 2 ab b2 ) 9a3 b3 = (a b) (a 2 ab b2 ) 10(a b)2 (a b) 2 = 4ab 11(a b)2 (a b) 2 = 2(a 2 b2 ) 12If a b c =0, then a3 b3 c3 = 3 abc INDICES AND SURDS 1 am a n = a m n 2



Algebra Formula Definition Formulas And Examples



Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf
$$(a b c)^3 = (a^3 b^3 c^3) (3a^2b 3a^2c 3abc) (3ab^2 3b^2c 3abc) (3ac^2 3bc^2 3abc) 3abc$$ $$(a b c)^3 = (a^3 b^3 c^3) 3a(ab ac bc) 3b(ab bc ac) 3c(ac bc ab) 3abc$$A 4 – b 4 = (a – b)(a b)(a 2 b 2)`(ab)^n=` `a^nna^(n1)b` `(n(n1))/(2!)a^(n2)b^2` `(n(n1)(n2))/(3!)a^(n3)b^3` `b^n` This can be written more simply as ( a b ) n = n C 0 a n n C 1 a n −1 b n C 2 a n −2 b 2 n C 3 a n −3 b 3 n C n b n
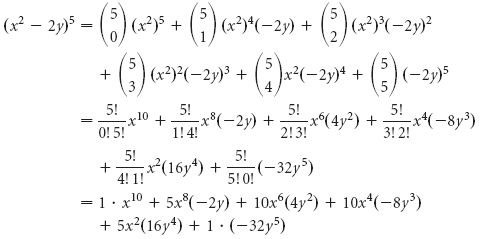


The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets



I Am Taking A Taylor Series Expansion Of A Function F X I Wish To Expand The Function Around The Value G X Is This Allowable
Popular Answers (1) 5th Feb, 16 Ioulia N Baoulina a 3 b 3 c 3 3abc= (ab) 3 3a 2 b3ab 2 c 3 3abc = (abc) 3 3 (ab) 2 c3 (ab)c 2 3ab (abc) = (abc) 3 3 (ab)c (abc)3ab (aWhat Is The Expansion Of A B C 3 Quora For more information and source, see on this link https//wwwquoracom/Whatistheexpansionofabc3Thermal expansion is large for gases, and relatively small, but not negligible, for liquids and solids Linear thermal expansion is ΔL = αLΔT, where ΔL is the change in length L, ΔT is the change in temperature, and α is the coefficient of linear expansion, which varies slightly with temperature



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo
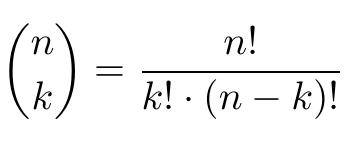


Binomial Coefficient Calculator
What I want to do with this video is cover something called the triple product expansion or Lagrange's formula, sometimes And it's really just a simplification of the cross product of three vectors, so if I take the cross product of a, and then b cross cA 3 b 3 c 3 3abc = (a b c) (a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3 3abc = (a b c) (a 2 b 2 c 2 ab bc ca) and we getThe scalar triple product is unchanged under a circular shift of its three operands (a, b, c) ⋅ (×) = ⋅ (×) = ⋅ (×)



Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf



Graph Graph Equations And Equation Systems With Step By Step Math Problem Solver
= (a b)(a b)(a b) = (a b)(a² ab ab b²) = (a b)(a² 2ab b²) = a³ 2a²b ab² a²b 2ab² b³ = a³ 3a²b 3ab² b³ Answer a³ 3a²b 3ab² b³= (a b)(a b)(a b) = (a b)(a² ab ab b²) = (a b)(a² 2ab b²) = a³ 2a²b ab² a²b 2ab² b³ = a³ 3a²b 3ab² b³A³ a²b a²c 2a²b 2ab² 2abc 2a²c 2abc 2ac² ab² b³ b²c 2abc 2b²c 2bc² ac² bc² c³ This is just multiplying out and bookkeeping It's a^3 b^3 c^3 plus 3 of eachAdding like terms, the final formula (worth remembering) is (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ac Practice Exercise for Algebra Module on Expansion of (a b c) 2


2



Proof Of Formula Of Whole Cube Of A B C A B C 3 Youtube
5(a b c)2 = a2 b2 c2 2ab2bc 2ca 6(a b c)3 = a3 b3 c33a2b3a2c 3b2c 3b2a 3c2a 3c2a6abc 7a2 b2 = (a b)(a – b ) 8a3 – b3 = (a – b) (a 2 ab b2 ) 9a3 b3 = (a b) (a 2 ab b2 ) 10(a b)2 (a b) 2 = 4ab 11(a b)2 (a b) 2 = 2(a 2 b2 ) 12If a b c =0, then a3 b3 c3 = 3 abc INDICES AND SURDS 1 am a n = a m n 2So the answer is 3 3 3 × (3 2 × x) 3 × (x 2 × 3) x 3 (we are replacing a by 3 and b by x in the expansion of (a b) 3 above)A³ b³ = (a b)(a² – ab b²) you know that (a b)³ = a³ 3ab(a b) b³ then a³ b³ = (a b)³ – 3ab(a b) = (a b)(a b)² – 3ab = (a b)(a² 2ab b² – 3ab) = (a b)(a² – ab b² ) Please log inor registerto add a comment Related questions


What Is The Formula For Math A B C 3 Math Quora



How To Expand Using The Identity A B C 2 B2 C2 2ab 2bc 2ca Youtube
Adding like terms, the final formula (worth remembering) is (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ac Practice Exercise for Algebra Module on Expansion of (a b c) 2A3 3a2b 3ab2 b3 Now, notice the exponents of a They start at 3 and go down 3, 2, 1, 0 Likewise the exponents of b go upwards 0, 1, 2, 3 If we number the terms 0 to n, we get this k=0 k=1 k=2 k=3(a b) 3 = a 3 b 3 3ab(a b) (a – b) 3 = a 3 – 3a 2 b 3ab 2 – b 3 = a 3 – b 3 – 3ab(a – b) a 3 – b 3 = (a – b)(a 2 ab b 2) a 3 b 3 = (a b)(a 2 – ab b 2) (a b) 4 = a 4 4a 3 b 6a 2 b 2 4ab 3 b 4 (a – b) 4 = a 4 – 4a 3 b 6a 2 b 2 – 4ab 3 b 4;



Document



Expansion Formulae Full Chapter 5 Std 8th I Expansion Formula Class 8th I Maths Chapter 5 Std 8th Youtube
(b)If exactly one member must be a woman, there are C(3;1)C(16;3) = 3560 = 1680 ways to form the committee (c)All of the committees formed in (b) qualify except those in which Smith and Jones are both members There are C(3;1)C(14;1) = 42 committees that both Smith and Jones can serve on, so C(3;1)C(16;3) C(3;1)C(14;1) = 1680 42 = 1638 committees canAccording to this theorem, it is possible to expand the polynomial \((x y)^n\) into a series of the sum involving terms of the form a \(x^b y^c\) Here the exponents b and c are nonnegative integers with condition that b c = n Also, the coefficient of each term is a specific positive integer depending on n and b For example (for n = 4), we have \((xy)^4=x^44x^3y6x^2y^24xy^3y^4\) It is obvious that such expressions and their expansions would be very painful to multiply out by handThermal expansion is large for gases, and relatively small, but not negligible, for liquids and solids Linear thermal expansion is ΔL = αLΔT, where ΔL is the change in length L, ΔT is the change in temperature, and α is the coefficient of linear expansion, which varies slightly with temperature


A 3 B 3 C 3



Expanding Algebraic Expressions Using Identities Worksheets
Take a = 2 x and b = 5 y, and replace them in the expansion of the formula for calculating the value in mathematical form ( 2 x − 5 y) 2 = ( 2 x) 2 ( 5 y) 2 − 2 ( 2 x) ( 5 y) ( 2 x − 5 y) 2 = 4 x 2 25 y 2 − 2 × 2 x × 5 y ∴ ( 2 x − 5 y) 2 = 4 x 2 25 y 2 − x y ( 2) Simplify 9 m 2 16 n 2 − 24 m n(a – b – c) 2 = a 2 b 2 c 2 – 2ab 2bc – 2ca (a b) 3 = a 3 3a 2 b 3ab 2 b 3;Property is if a b c = 0 then a 3 b 3 c 3 = 3abc (i) a = 13, b = 8 and c = 5 13 3 (8) 3 (5) 3 = 3(13)(8)(5) = 1560 (ii) a = 7, b = 3, c = 10 7 3 3 3 (10) 3 = 3(7)(3)(10) = 630 (iii)a = 9, b = 5, c = 4 9 3 5 3 4 3 = 9 3 (5) 3 (4) 3 = 3(9)(5)(4) = 540 (iv) a = 38, b = 26, c = 12 38 3 (26) 3 (12) 3 = 3(38)(26)(12) =


Http Www Cpp Edu Jjnazareth Phy122l132l Prelabcle Pdf



Solved 6 Find The Following Determinants Using The Cofac Chegg Com
A 4 – b 4 = (a – b)(a b)(a 2 b 2)Ex a b, a 3 b 3, etc Binomial Theorem Let n ∈ N,x,y,∈ R then n Σ r=0 nC r x n – r · y r nC r x n – r · y r nC n1 x · y n – 1 nC n · y n ie(x y) n = n Σ r=0 nC r x n – r · y r where, Illustration 1 Expand (x/3 2/y) 4 Sol Illustration 2 (√2 1) 5 (√2 − 1) 5 Sol We have(a – b – c) 2 = a 2 b 2 c 2 – 2ab 2bc – 2ca (a b) 3 = a 3 3a 2 b 3ab 2 b 3;



What Are Various Forms To Write A B C A Whole Cube Quora



Hw3 Solution
We can choose an a in 3 ways, and then a b in 2 ways, and then we have only one way to choose a c The coefficient is therefore 3·2·1=6 Finally, add up the coefficients to check they come to (111) 3 =27Solution We have (a b) n, where a = 2/x, b = 3√ x, and n = 4 Then using the binomial theorem, we have Then using the binomial theorem, we have Finally (2/x 3√ x ) 4 = 16/x 4 96/x 5/2 216/x 216x 1/2 81x 2Once you get above the fourth power, the algebra becomes tedious You don't have to calculate these out completely though there's a shortcut of sorts The formula gives the expansion of any binomial series, but you'll still have to work through some algebra to actually expand it


Www Shsu Edu Kws006 Math History 2 The Greek Age Files 2 Ws Greekage Pdf


What Is The Formula For Math A B C 3 Math Quora
I could never remember the formula for the Binomial Theorem, so instead, I just learned how it worked I noticed that the powers on each term in the expansion always added up to whatever n was, and that the terms counted up from zero to nReturning to our intial example of (3x – 2) 10, the powers on every term of the expansion will add up to 10, and the powers on the terms will increment byA 3 b 3 c 3 3abc = (a b c) (a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3 3abc = (a b c) (a 2 b 2 c 2 ab bc ca) and we getA1/3 a1/3 a1/3 = a (24) (a1/3)3 = a (25) (a2)1/3 = (a1/3)2 = a2∕3 (26) (a1/3)1/4 = a1/3 1/4 = (a1/4)1/3 (27) (a b)1/3 = a1/3 b1/3 (28) (a / b)1/3 = a1/3 / b1/3 (29) (1 / a)1/3 = 1 / a1/3 = a1/3 (30) Sponsored Links Mathematics Mathematical rules and laws numbers, areas, volumes, exponents, trigonometric functions and more


Academic Oup Com Ptp Article Pdf 13 4 405 13 4 405 Pdf


What Is The Formula Of Math A 3 B 3 Math Quora



Solved 2 We Ve Studied The Binomial Theorem In Class In Chegg Com


Standard Identities Of Binomials And Trinomials Equations Examples
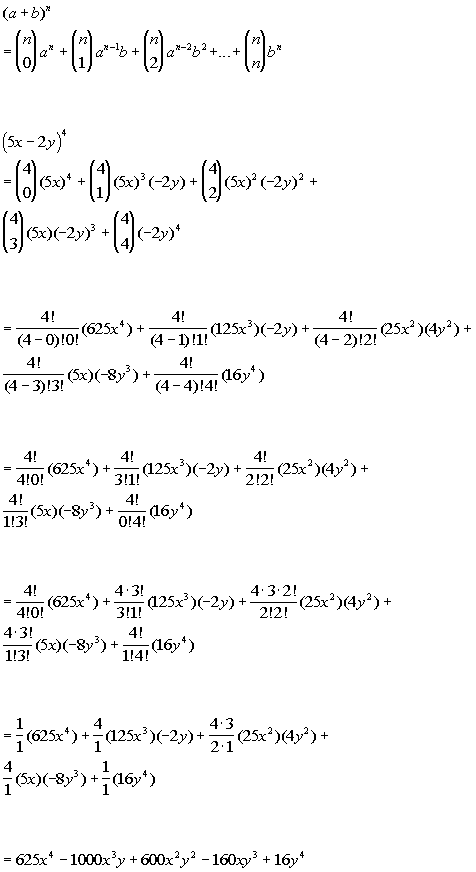


Wtamu Math Tutorials And Help



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets



Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf



Expansion Archives Sat Prep


Search Q A B 5e3 Tbm Isch


What Is The Expansion Of A B C 3 Quora


2



Misc 2 Without Expanding The Determinant Prove That Miscellaneous



Pascal S Triangle And The Binomial Theorem X Y 0 1 X Y 1 1x 1y X Y 2 1x 2 2xy 1y 2 X Y 3 1x 3 3x 2 Y 3xy 2 1 Y 3 X Ppt Download



A What Is The Expansion Formula For A B 2 4



Vector Triple Product Expansion Very Optional Video Khan Academy


2


Factorials To Binomial Theorem



Binomial Theorem



Binomial Theorem Wikipedia



Using The Properties Of Determinants Prove That A B B C C A A3 C3 Pls Note It Is C Instead Of I Mathematics Topperlearning Com 8xllr9tt



A B C Whole Cube A Cube B Cube C Cube 3 A B B C C A Prove It Plzzzz I Need It Today Brainly In
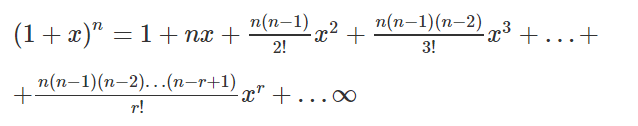


Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf



Taylor Series Expansion


Pascal S Triangle And Binomial Expansion Video Khan Academy



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets



54 Mcqs For Homework 3 Principles Of Chemistry I Chem 1307 Docsity



Misc 1 Find A B N In Expansion Of A B N If First Three



Document
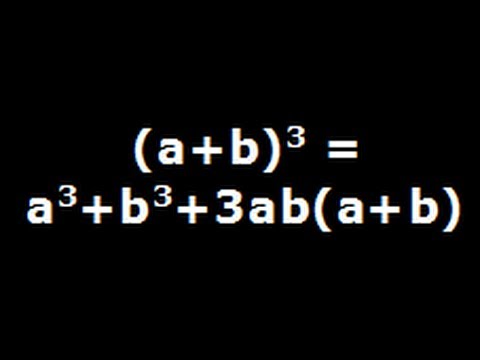


A Plus B Cube Algebra Identity Explained Step By Step Youtube


Factorials To Binomial Theorem


Search Q Algebra Formula Chart Tbm Isch



Triple Product Wikipedia



Solved A Let N 3 Expand Out All The Terms In This Expr Chegg Com


What Is The Expansion Of A B C 3 Quora



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo


What Is The Expansion Of A B C 3 Quora


Q Tbn And9gcrwxskagpy6lndt5stu6oxp1 K0tw6brabfeaf Ncwojlvhrcb Usqp Cau


4 The Binomial Theorem


What Is The Formula For Math A 3 B 3 Math Quora


What Is The Expansion Of A B C 3 Quora


What Is The Value Of A B C 3 Quora



Binomial Expansion Exam Solutions C2 Examples Worksheets Videos Activities



Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab



Show Working For A B And C Please For B The Q Chegg Com


Solution Use The Binomial Theorem To Expand The Binomial And Express The Result In Simplified Form X 4 3



What Are Various Forms To Write A B C A Whole Cube Quora



Standard Identities Of Binomials And Trinomials Equations Examples
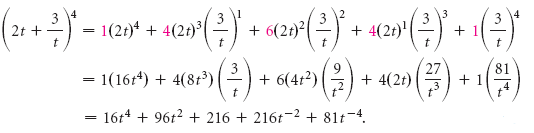


The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets
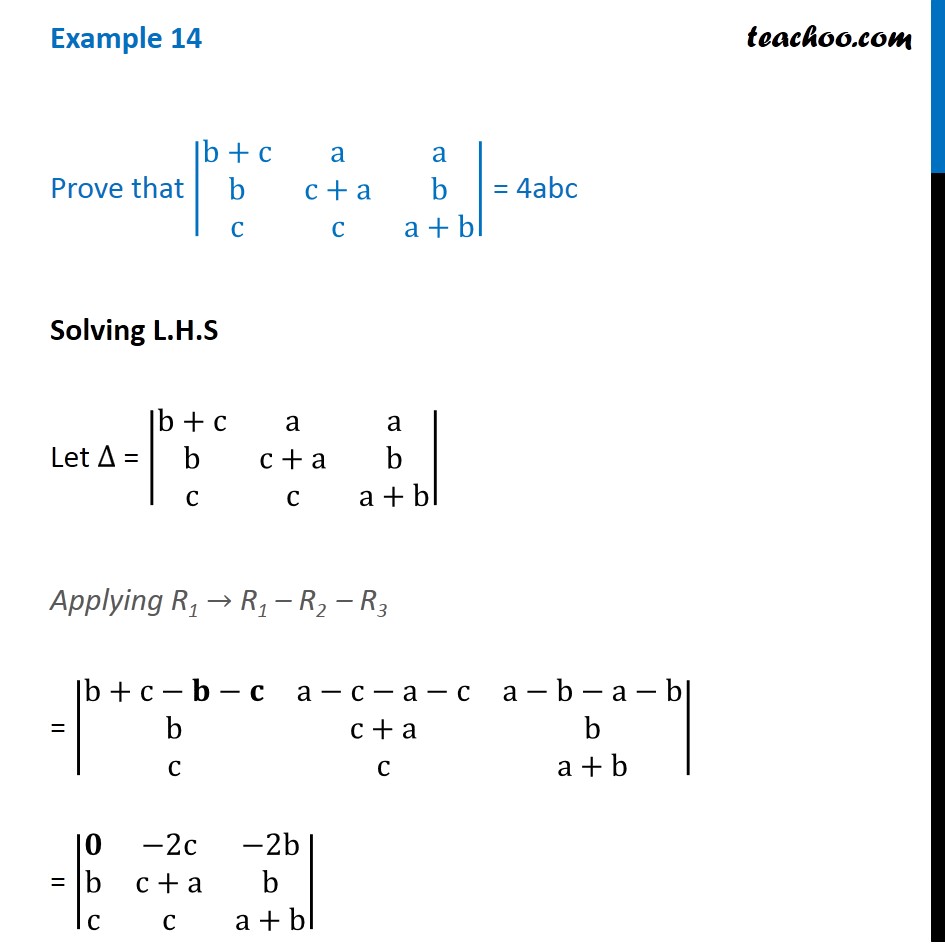


Example 14 Prove That B C A A B C A B C C A B 4abc
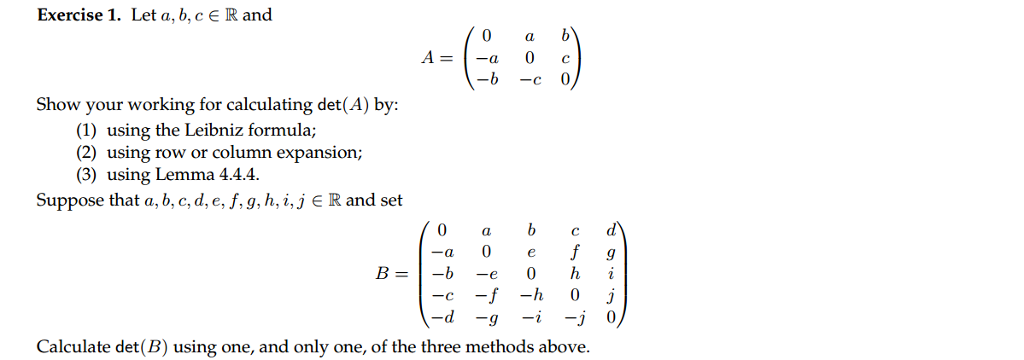


Solved Exercise 1 Let A B Cerand A 0 C Show Your Work Chegg Com



Msbshse Solutions For Class 8 Maths Part 1 Chapter 5 Expansion Formulae Download For Free


What Is The Expansion Of A B C 3 Quora



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets


2
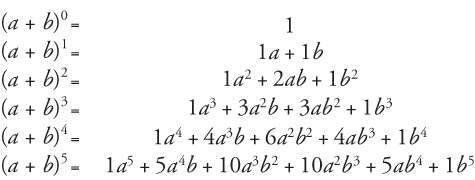


Binomial Coefficients And The Binomial Theorem
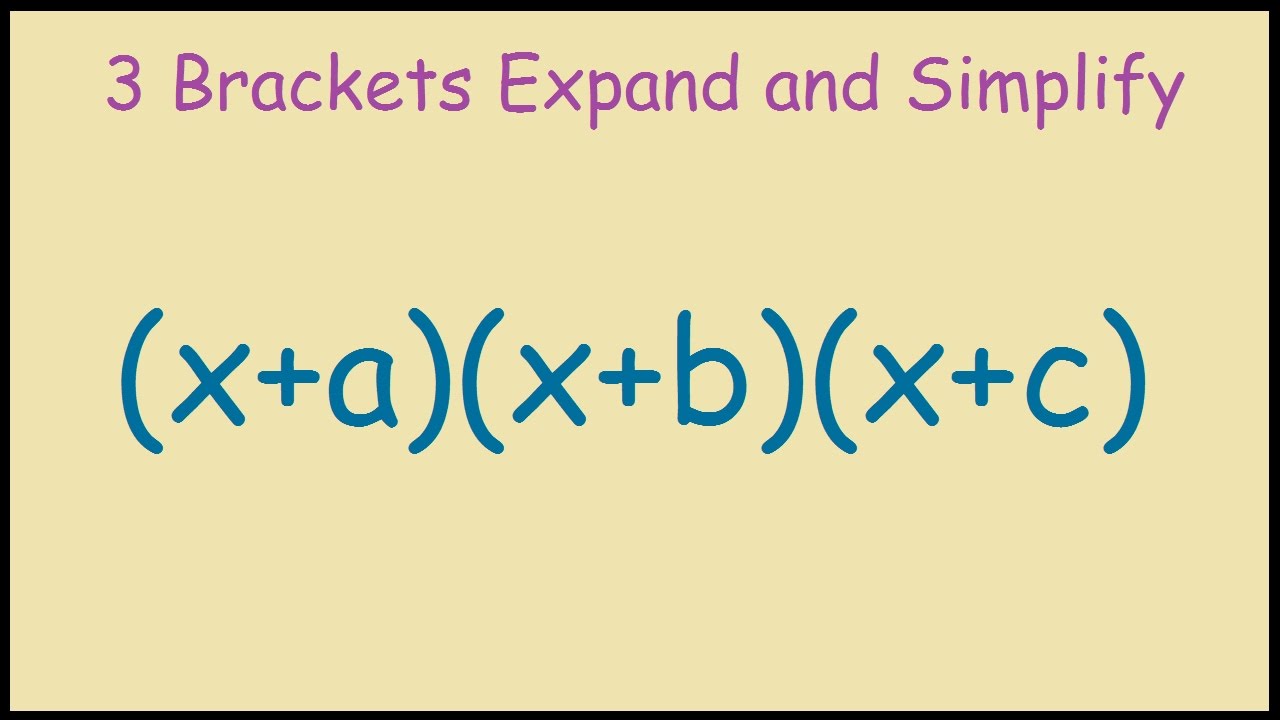


X A X B X C Expand And Simplify Youtube


2



Binomial Theorem For Any Index



A B N And A B N Formula Expander



What Is The Expansion Of A B C 3 Quora



Solved 2 Use The Table Of Laplace Transform In The Formu Chegg Com


Www Eee Hku Hk Engg1015 Fa11 Handouts 07 Digitallogic



Foil Method Wikipedia



Solved A A 3 2 32 Let A B 5 4 And B B 5 4 Find Det A Chegg Com



Vector Triple Product Definition Formula Proof Solved Problems



What Are Various Forms To Write A B C A Whole Cube Quora



Intro To The Binomial Theorem Video Khan Academy



General And Middle Term Binomial Theorem Formula Videos Examples



Multinomial Expansion



The Value Of A Cube Plus B Cube Plus C Cube Minus 3 Abc If A B C Is Equals To 15 And A B Ca Brainly In


What Is The Expansion Of A B C 3 Quora


Factorials To Binomial Theorem



Expand The Following A 3b C 2 Brainly In



Expanding Algebraic Expressions Using Identities Worksheets



Binomial Theorem Wikipedia



What Are Various Forms To Write A B C A Whole Cube Quora


コメント
コメントを投稿